Higer order bows | Keaoakua

Higher Order Rainbows

Features of higer order rainbows

Higer order bows are those with 3 or more arcs. There is no definition within the Hawaiian dictionary for these types.

Primary trait: A rainbow with 3 or more arcs

Secondary trait: A rainbow with the majority of the color

A third order bow (na shutterstock)

These types of rainbows are indeed extraordinary, however they do appear in some traditional Hawaiian stories, and have also been witnessed by some people here in Hawaii. In the western scientific perspective, witnessing a rainbow with 3 arcs or more is extremely rare. A three arc rainbow is shown above,[1] however the authenticity of this photo may be in question. Finding photographs of higher order rainbows is very difficult due to their scarce appearance.

The order of the rainbow is determined by the number of reflections of the light within the water drops. A primary rainbow is also called a first order rainbow, a double rainbow is also called a secondary rainbow, a rainbow with 3 arcs is a third order, etc.[2]

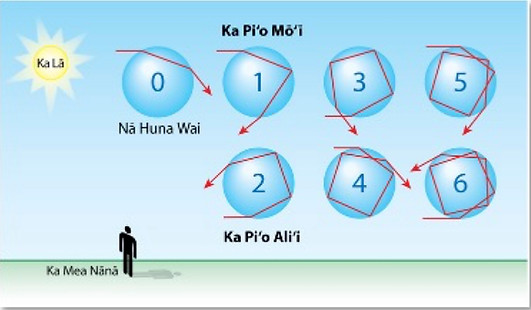
The rainbow colors are seen as a result of the light rays being directed toward the observer. This can be seen in the diagram above. In other words the observer is able to see the first, second, fifth, and sixth order rainbows. The zeroth, third, and fourth orders are directed away from the observer.[3] Witnessing any higher level rainbow is extremely rare, however, a fifth order was photographed in 2009.[4] The zeroth order rainbow appears behind the observer and is not a true rainbow. It is called a zeroth order glow.[5]

Sometimes, several color bands can be seen below the primary rainbow (Piʻo Mōʻī) and above a secondary arc (Piʻo Aliʻi), these are called supernumerary bows (Piʻo pēpē).[6] These arcs are typically violet and green. The size and spacing of these arcs is variable. These are shown in the pictures below.

Supernumerary bows (na Andrew Hara).

In the scientific view, the reason for the appearance of the supernumerary bows is

I ke kuanaʻike ʻepekema, ʻo ke kumu o ka ʻōʻili ʻana o ia mau ʻauina makawalu, ʻo ia kekahi mau ʻauina ʻākeʻakeʻa. Kaukaʻi ka ʻōʻili ʻana o nā ʻauina makawalu ma ka nui o nā huna wai o ka Piʻo Mōʻī a me ka nui like o nā huna wai i lalo pono o ka Piʻo Mōʻī.[11] Neʻe kekahi mau kukuna malama i loko o nā huna wai i kahi ala ʻokoʻa iki, a no ia mea, he puka mai nō ia ma o kekahi mau huina ʻokoʻa iki. ʻO ka hopena, ʻo ia ka ʻākeʻakeʻa kūkulu a me ka ʻākeʻakeʻa luku o kekahi mau waihoʻoluʻu malama. A no ia mea, ʻōʻili ia mau ʻauina makawalu ma lalo pono o ka Piʻo Mōʻī. ʻO ka mea maʻamau, lolilua ko nā huna wai nui ma kahi o ka Piʻo Mōʻī e ʻōʻili ana, a no laila, nalowale nā ʻauina makawalu. I nā manawa o ka ʻauina makawalu e ʻōʻili ai, hūnā ʻia ka hapa nui o nā waihoʻoluʻu i ka ʻākeʻakeʻa ʻia.[12] A no ia mea, ʻike pinepine wale ʻia ka ʻōmaʻomaʻo a me ka mākuʻe. Wehewehe ʻia nā ʻauina makawalu i ke kuanakuhi hawewe o ka malama.[13] Hiki ke ʻike ʻia ka ʻauina makawalu i nā Kiʻi ma luna aʻe.

Nā pōʻai lewa o nā piʻo ānuenue kūlana kiʻekiʻe e ʻōʻili ai

Ua like paha nā pōʻai o nā piʻo ānuenue kūlana kiʻekiʻe me ko ka piʻo ānuenue pālua, ʻo ia hoʻi ka lewa lani lewa, ka lewa nuʻu, a me ka lewa lani. Eia naʻe, ma muli o ko lākou ʻike kākaʻikahi ʻia, paʻakikī ka mahuʻi ʻana i nā pōʻai lewa o lākou e ʻōʻili ai.

Nā manawa o ke ānuenue kūlana kiʻekiʻe e ʻōʻili ai

I loko nō o ka ʻike ʻepekema e pili ana i ke anahonua kikoʻī no ka ʻōʻili ʻana o nā ānuenue kūlana kiʻekiʻe, ʻike ʻia ua mau ānuenue nei e kekahi mau mea nānā i kauwahi manawa ʻē aʻe. He moʻolelo hoihoi ko kekahi kumu e pili ana i ka ʻōʻili ʻana i kekahi piʻo ānuenue ʻekolu. I ka makahiki 1991, ma hope o ka hala ʻana o ka makani pāhili ʻo ʻIniki i kēia pae ʻāina nei, a ma hope nō hoʻi o ka pouli holoʻokoʻa ʻana o ka lā, e kūkulu ana lāua ʻo kona ʻohana i kekahi lele nona ʻekolu haka ma ka heiau ʻo Puʻuina ma ka moku o Keawe. I loa nō iā lākou a hīkiʻi i ke aho hope loa o nā pou, a ma hope koke o ka hiki ʻana o ka lā ma ke kūlana ʻo Kahikikapuihōlanikekuʻina (awakea), ua ka ua kilihune. Eia naʻe, mālaʻe ka lewa, ʻaʻohe ao. ʻO ko lākou ʻike leʻa ihola nō ia i kekahi ānuenue pākolu. Ua noʻonoʻo ʻia he wānana maikaʻi ma muli o kā lākou kūkulu ʻana i ia lele.[14] He laʻana maikaʻi loa ia o ka ʻōʻili ʻana i kahi ānuenue kūlana kiʻekiʻe i kekahi manawa kūʻē i ka ʻike ʻepekema. Manaʻo ʻia ma ʻike ʻepekema, ʻaʻole hiki ke ʻike maka ʻia ia mau piʻo ānuenue kūlana kiʻekiʻe ma muli o ke anahonua a me ke kālaikūlohea ma loko o nā huna wai. Akā, kū nō kēlā i ka ʻike Hawaiʻi.

Nā hōʻailona o ka piʻo ānuenue kūlana kiʻekiʻe

ʻEkolu hōʻailona like ʻole o ka piʻo ānuenue kūlana kiʻekiʻe ma loko o nā kūmole i kālailai ʻia. Hōʻike ʻia ma loko o ka Pakuhi o luna aʻe. Aia he ʻehiku o ia mau hōʻailona ma loko o nā kūmole like ʻole. He ʻehā ka huinanui o nā hōʻailona pili i ke kū ʻana. Ua hoʻohana hou ʻia ia hōʻike haʻihelu hoʻoili no ka hoʻomaopopo ʻana i ka huinanui o ia mau hui hōʻailona ʻekolu e pili ana kekahi i kekahi. ʻO ka hopena o ia hōʻike haʻihelu hoʻoili, ua ʻāpono ʻia ke kuhiakau kūpapa.[15] No laila, ʻaʻole ʻoi aku ka huinanui o kekahi mau hui hōʻailona ma mua o nā hui hōʻailona ʻē aʻe. E hōʻike ʻia kekahi mau laʻana hōʻailona o ka piʻo ānuenue kūlana kiʻekiʻe o lalo iho.

[1] Kākaʻikahi nō ke ānuenue pākoli, a no laila, malia paha, hoʻololi ʻia kēia kiʻi i mea e hōʻike ai i nā piʻo he ʻekolu.

[2] n.d. Higher Order Bows. Accessed 4 2024. https://atoptics.co.uk/blog/higher-order-bows/.

[3] Harold Edens. 2015. "Photographic observation of a natural fifth-order rainbow." Applied Optics (Optical Society of America) 54 (4): B26-B34.

[4] n.d. Higher Order Bows. Accessed 4 2024. https://atoptics.co.uk/blog/higher-order-bows/.

[5] John A. Adam. 2002. "The mathematical physics of rainbows and glories." Physics Reports (Elsevier) 356 (4-5): 229-365. Accessed ʻApelila 2024.

[6] n.d. Higher Order Bows. Accessed 4 2024. https://atoptics.co.uk/blog/higher-order-bows/.

[13] Carl B. Boyer (1987). The Rainbow: From Myth to Mathematics. Princeton, NJ: Princeton University Press.

[14] Māhealani Pai, ua nīnauele ʻia e Hoaloha Westcott. 2024. ʻIke ānuenue (Mei 14).

[15] Frederick J. Gravetter and Larry B Wallnau. 2013. Essentials of Statistics for the Behavioral Sciences. 8. Wadsworth Cenegage Learning. ʻaoʻao 518. E nānā ʻia i ka Pākuʻina 1 no kekahi hoʻākaaka ʻana e pili ana i kēia hōʻike makemakika. ʻO ka hopena o ka hōʻike haʻihelu hoʻoili: χ2 (2, n = 7) = 2.0, p < 0.735. No laila, ʻapono i ke kuhiakau kūpapa.

na Kelly Headrick | Dreamstime.com