​Features of the double rainbow

​

There is no specific definition for the double rainbow in the dictionaries.  Therefore the definition of the Piʻo Ānuenue will be used here:  According to the Hawaiian-English dictionaries, this is the definition o this type of rainbow:[1]

​

Pukui/Elbert:       1. nvs., Arch, arc; bent, arched, curved; to arch, of a rainbow.

Parker:                1. v., To be bent; to be curved; to bend around as the arch of a                                                        rainbow; to curve as an arch; to bend as an elastic substance.

​

Primary trait:             A rainbow with 2 arches

Secondary trait:        A rainbow with the majority of all the rainbow colors

 

​

​

​

​

​

​

​

​

​

​

​

​​

​

​​

An interesting question perhaps, are there names for the two arches in Hawaiian culture. Two naming systems were found. Refer to the picture below. In the first system, the inside arch is called the Piʻo Tuahine and has female energy. In this arch the red is on the outside and the violet is on the inside. This arch is associated with the kūpaʻa rain. The arch on the outside is called the Piʻo Kūnohu and has male energy. In this arch, the violet is on the outside and the red is on the inside, i.e. the colors are reversed. This arch is associated with the Lanipili rain. Sometimes multiple arches appear below the Piʻo Tuahine, these are called the Piʻo Pēpē (baby arches). These arches are associated with the kilihune rain.[3] See the page on higher order bows on this website for more information on the Piʻo Pēpē.

​

In the second naming system, the inside arch is called the Piʻo Mōʻī, and the outside arch is called the Piʻo Aliʻi. According to Joseph Nāwahī, the order of these names is due to the positions of the Mōʻī (ruling chief) and the Aliʻi (subordinate chiefs) within certain heiaus.[4] There is no name that corresponds to the Piʻo Pēpē in this system. These two systems are shown in the picture below.

​

The naming systems of the arches 

​

​

​

​

​

​

​

​​

​

​

​

 

​

Is one of these two naming system better than the other? Perhaps the systems were used in different locations, such as different islands or different districts within one island. Neither system is superior to the other, they are just different ways to refer to the beautiful double rainbow.​​​​​​

​

​

​

​

​

​

​

​

​

​

​

​

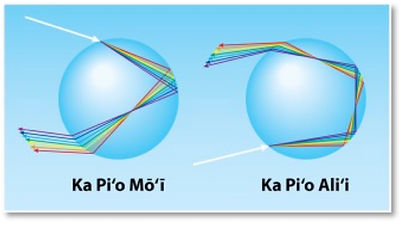
There are some very interesting features of the double rainbow. The first was discussed on the full arching rainbow, specifically, the inside of the Piʻo Mōʻī is brighter than the outside. The next is that the brightness of the Piʻo Mōʻī is roughly 3 times that of the Piʻo Aliʻi. Between the two archs is a dark region called Alexanderʻs dark band.[5] Alexander of Aphrodisias was the first to explain this band in the year 200 AD.[6] Some of the sun rays in this area do not reflect and so this band appears darker.[7] The order of colors is reversed in the Piʻo Aliʻi, why is this? For the Piʻo Mōʻī, the sun rays enter the water drops, the white light is separated into the colors because of refraction, the travel to the back of the water drop and are reflected back to the front of the drop and then exit to form the Piʻo Mōʻī at an angle of 40-42 degrees. Therefore the Piʻo Mōʻī forms as a result of one reflection inside the water drops. For the Piʻo Aliʻi, the light colors reflect a second time  within the water drops before emerging to form the arch at an angle of 50-54 degrees.[8] These effects are shown in the diagrams below.​​​​​

 

The angles of the primary and secondary rainbows                         The reflections within water drops

​​

​

​

​

​

​

​

​

​

​

​

​

​​

​

The Piʻo Aliʻi (secondary arch) is located approximately 10 degrees outside of the Piʻo Mōʻī (primary arch). The center of both archs are at the same point which means that the diameter of the secondary arch is approximately 1.8 times that of the primary arch.​​​​​​​​​​

 

The sky strata that the double rainbow appears

​​​​​

The angles of the primary and secondary rainbows

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

​

Joseph Nāwahī understood the angles of the primary (40-42 degrees) and secondary (50-54 degrees) archs.[9] By using the aforementioned angles as well as some geometry, the altitudes of the arcs can be estimated. If the double rainbow appears above the horizon (approximately 3.1 miles from the observer at sea level), and the sun is at the position of Kahikikū, approximately 2.79 miles (14,731 feet) would be the altitude of the primary rainbow, and 4.27 miles (22,544 feet) would be the altitude of the secondary arch. Since the lewa lani strata is from 14,500 -  60,000+, the tops of the primary and secondary rainbows would be in the lewa lani in this example. The picture above showing the names of the arcs is perhaps an shows an example. Sometimes, the double rainbow is close to the earth as shown in the picture below. The primary arc is on the horizon and perhaps only half of itʻs width can be seen. Therefore the top of the primary arc is approximately 340 feet above the horizon (based on the average width of a rainbow) and is in the lewa lani lewa. The distance between the top of the primary arc and the secondary arc is approximately 7,800 feet. Therefore, the top of the secondary rainbow ia approximately 8,140 feet (340 + 7,800 = 8,140) and is therefore in the lewa nuʻu strata.

​

Double rainbow close to the ocean  (na Tianne Alegnani ke kiʻi)

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​​​​

Times that the double rainbow appear

 

When the sun passes above 42 degrees above the horizon, primary rainbows disappear below the horizon. When the sun angle exeeds 54½ degrees, secondary rainbows disappear below the horizon.[9] When the sun exceeds the above angles, it is in Kahikikapuihōlanikekuʻina. Ua ʻike ʻia ia mau mea e Joseph Nāwahī, a ʻike ʻia nō hoʻi e nā mea ʻepekema o kēia au nei.

​

Signs/Omens of the double rainbow

 

​There were 5 signs/omens of the double rainbow found in the sources analyzed for this project. These are shown in the table below.​

​

There were 5signs/omens found within the sources analyzed for the double rainbow. There are 9 occurrences of these signs/omens, and the signs concerning a presence were the most numerous (4). The Chi-square goodness-of-fit test was performed on the data, and the result is that the data does not vary significantly from an equal distribution and therefore none of the groups is significantly different than the others from a mathematical perspective. Examples of these signs/omens are not available at this time in English but are shown on the Hawaiian side of the website. 

​

​

​

​

​

​

​

​

​

​

​

 

 

 

 

 

 

 

 

 

​​​​​​

​Translation Key

​

​

​

​

​

​

​

​

​

​

​

​

​

​​

​

​

​​​​​​​​​​​​

​​

​

​

[1] n.d. Wehewehe Wikiwiki. Ke Kulanui o Hawaiʻi ma Hilo. https://hilo.hawaii.edu/wehe/.

[2] Joseph Nawahi, "Ke Anuenue a me Ka Luakalailani." Ka Leo o ka Lahui, Mei 24, 1893: 2-3.

[3] Jeana Naluwai. Ua nīnauele ʻia e Hoaloha Westcott. 2022. ʻIke ānuenue (Nowemapa 14).

     Mika Lee, interview by Anthony Aalto. 2013. Hana Hou Magazine: Signs and Wonders Hana Hou Magazine, (January).​

[4] Joseph Nawahi, "Ke Anuenue a me Ka Luakalailani." Ka Leo o ka Lahui, Mei 24, 1893: 2-3. Hōʻoia ʻia nā ʻano o ka heiau ma loko o kā Kepelino puke: Kepelino, Z.K. 2007. Kepelinoʻs Traditions of Hawaiʻi. Honolulu, HI: Bishop Museum Press. ʻaoʻao 59.​

[5] John A. Adam. 2002. "The mathematical physics of rainbows and glories." Physics Reports (Elsevier) 356 (4-5): 229-365. Accessed ʻApelila 2024.

[6] Carl B. Boyer (1987). The Rainbow: From Myth to Mathematics.  Princeton, NJ: Princeton University Press. ʻaoʻao 294.

[7] k.l.

[8] Joseph Nawahi, "Ke Anuenue a me Ka Luakalailani." Ka Leo o ka Lahui, Mei 24, 1893: 2-3; John A. Adam. 2002. "The mathematical physics of rainbows and glories." Physics Reports (Elsevier) 356 (4-5): 229-365. Accessed ʻApelila 2024.

​[9] Joseph Nawahi, "Ke Anuenue a me Ka Luakalailani." Ka Leo o ka Lahui, Mei 24, 1893: 2-3;

​

​